Approfondimento Teorico (Forza Magnetica)
Una particella carica, il nostro pione negativo p. es. (\( \pi^-\)), si muove con una certa velocità \(\vec{v}\) in una regione in cui è presente un campo magnetico \(\vec{B}\) uniforme, perpendicolare alla sua velocità.
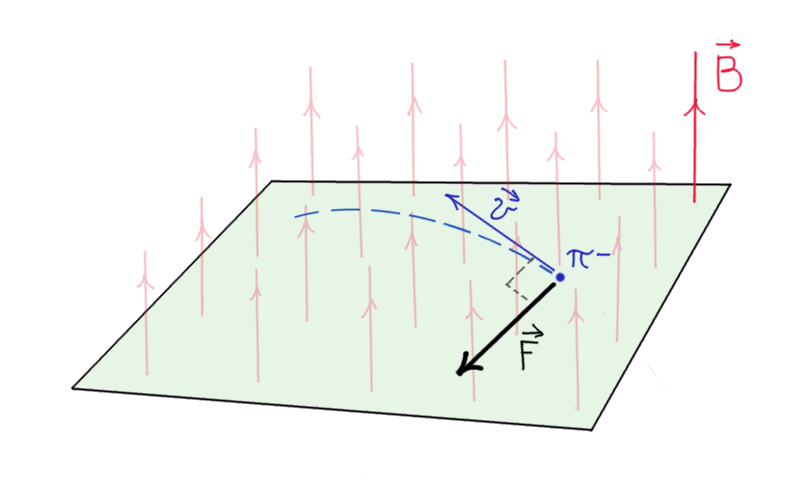
Come sappiamo sul pione agirà una forza \(\vec{F}\), di natura magnetica, data dalla relazione vettoriale:
\( \vec{F}=q\,\vec{v}\times \vec{B}\).
Il nostro pione si muove all’interno del rivelatore, una camera piena di gas d’He. Essendo carico, interagisce elettromagneticamente con gli elettroni degli atomi di He, ionizzandoli. La traccia che lascia nel rivelatore è proprio dovuta alla ionizzazione.
Visto che la forza magnetica agisce perpendicolarmente alla \(\vec{v}\) della carica e che possiamo trascurare le perdite energetiche imputabili alla ionizzazione, possiamo considerare costante il modulo della velocità del pione.
Dunque la situazione generale è quella di una particella carica che si muove in campo magnetico uniforme \(\vec{B}\perp \vec{v}\), con una velocità in modulo costante. In tal caso la forza magnetica ha le seguenti proprietà:
- \(\vec{F}\perp \vec{v}\)
- \(\vec{F}\) ha modulo costante
e può essere considerata una forza centripeta. Possiamo allora scrivere (ricordando che l’angolo tra \(\vec{B}\) e \( \vec{v}\) è di 90°):
\( qvB=m\frac{v^2}{r}\).
Da cui, semplificando la \( v\),
\( qB=\frac{p}{r}\)e infine:
\( p=qrB\)
Siamo giunti al cuore della questione. Una volta nota la carica \(q\) della particella e il valore del campo magnetico \(\vec{B}\), per valutare l’impulso occorre conoscere il raggio di curvatura \(r\) della sua traiettoria. È per questo motivo che i rivelatori sono immersi in campi magnetici di intensità nota e si continuano a sviluppare tecnologie per il tracciamento.