Conservazione della quantità di moto in 2D. Ecco come fare!

Quando due corpi interagiscono scambiano quantità di moto (qdm). Lo scambio avviene a tutte le scale, da quelle infinitamente piccole sub-nucleari alle nostre, fino ad arrivare a scale infinitamente grandi come quelle che separano gli oggetti che popolano il nostro Universo: i pianeti, le stelle, le galassie. E’ qualcosa di universale, intimamente legato al concetto di interazione. Il modello più accreditato che descrive le interazioni è il Modello Standard. Esso prevede che le interazioni possano essere di quattro tipi: nucleare forte, nucleare debole, elettromagnetica e gravitazionale. Insomma, è un po’ come se ci venisse detto che tutto ciò che accade può essere interpretato come un effetto di una di queste interazioni fondamentali o, forse sarebbe meglio dire, come un mix di queste. Comunque sia, ogni volta che dei corpi interagiscono assistiamo a un trasferimento di qdm da uno all’altro. Per inciso, la qdm è il prodotto della massa di un corpo per la sua velocità: $$m\vec{v}$$ Un principio fondamentale della Fisica afferma che la qdm totale che abbiamo prima che due o più corpi interagiscano è sempre uguale a quella che troviamo dopo l’interazione. Bisogna solo fare attenzione che la qdm è una grandezza vettoriale quindi, calcolando la qdm totale di più corpi non basterà sommare numeri, dovremmo sommare vettori!
Adesso ci concentriamo su come si possa introdurre questa legge a chi sta apprendendo la fisica. Lo faremo lavorando con semplici oggetti, che abbiamo sempre intorno a noi, ma che assemblati con un po’ di creatività diventano un vero e proprio laboratorio per studiare le interazioni tra corpi, perlomeno alle nostre scale. In un post successivo, che vi prometto sin da ora, vedremo come potremo estendere queste esplorazioni anche su scale sub-nucleari (quindi … antenne ben attive sulle prossime uscite di 2-Penny Physics!). Il bello di tutto ciò è che il laboratorio a cui sto pensando permette di lavorare in 2 dimensioni consentendo di toccare con mano la natura vettoriale della legge cui accennavo prima. Inoltre, il dispositivo di cui parlo pesa meno di 100g e costa ….beh …direi 2-Penny!
Per realizzarlo sono sufficienti 2 fogli di carta A4, una scatola di cartone, alta non più di 15 cm (le scatole dei cellulari sono più che ok), e 2 monete da 1 centesimo di euro. Ah dimenticavo, è anche green dal punto di vista energetico …l’alimentatore è la gravità terrestre.
Altro pregio è che può essere costruito sul banco di ogni studente o, alternativamente, a casa sulla propria scrivania. Coinvolge in un’esplorazione attiva e rende evidente la natura vettoriale del fenomeno.
Nel filmato di sopra potete vedere il “potente” apparato in azione! Questo video Tutorial vi mostra la conduzione dell’esperimento passo passo.
Per chi fosse interessato a saperne di più, da qui in avanti entriamo in dettagli più tecnici. Utili a chi vuole apprendere questa bellissima parte della Fisica o vuole saperne di più per poi portare il ‘2-Penny approccio‘ nella propria classe.
Dettagli tecnici … approfondiamo l’idea
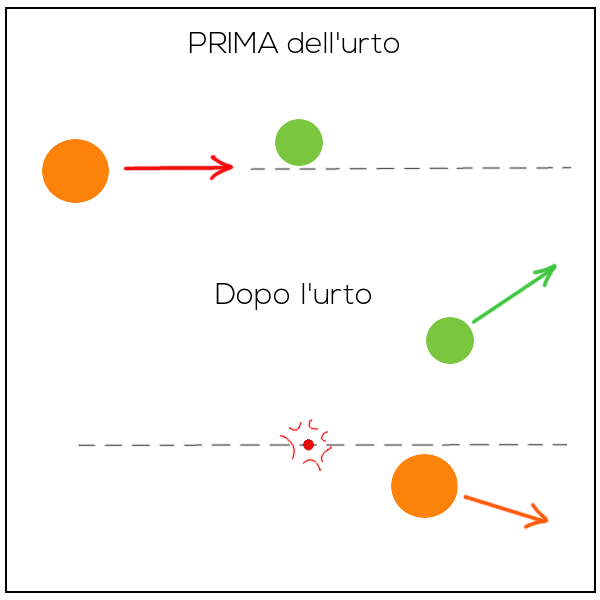
Per visualizzare uno scambio di qdm possiamo pensare a un urto tra 2 corpi. In genere, dopo l’interazione entrambi si muoveranno in direzioni diverse da quelle che avevano prima, ma la qdm del sistema formato dai 2 corpi prima dell’urto sarà identica a quella dopo l’urto. Per questo in fisica diciamo che la qdm si “conserva”. Mi spiego meglio. Prima di tutto devo ricordare che la qdm è una quantità vettoriale, cioè una grandezza che, oltre ad avere un valore numerico, ha una direzione e un verso. Per questo la rappresentiamo con una freccia. La direzione e il verso del vettore sono dati dalla velocità del corpo, la lunghezza rappresenta il valore numerico della qdm ed è data dal prodotto $$m\cdot v$$.
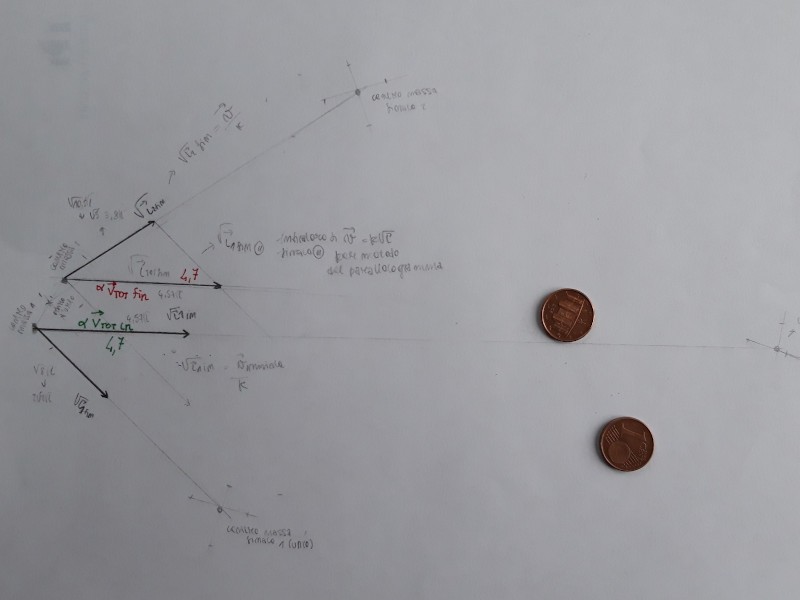
Nelle immagini vedete le qdm dei due corpi prima dell’urto (il corpo verde, in questo caso, è fermo quindi la sua qdm è nulla …a lui non associamo alcuna freccia). La qdm del sistema è la somma vettoriale delle qdm dei 2 corpi.
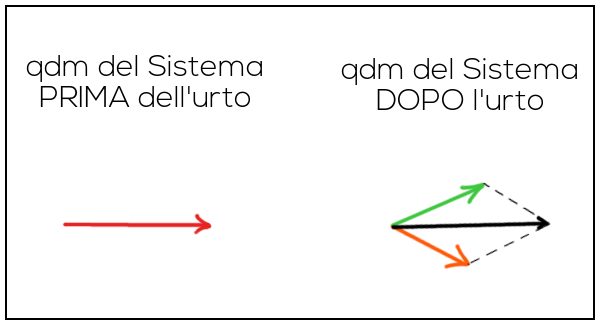
Quindi la qdm del sistema all’inizio è data dalla sola qdm del corpo incidente (vettore rosso), quella finale è la somma del vettore arancione e del vettore verde . Come vedete nella immagine qui sotto, i vettori ‘qdm del sistema’ prima e dopo l’urto si conservano, cioè sono uguali.
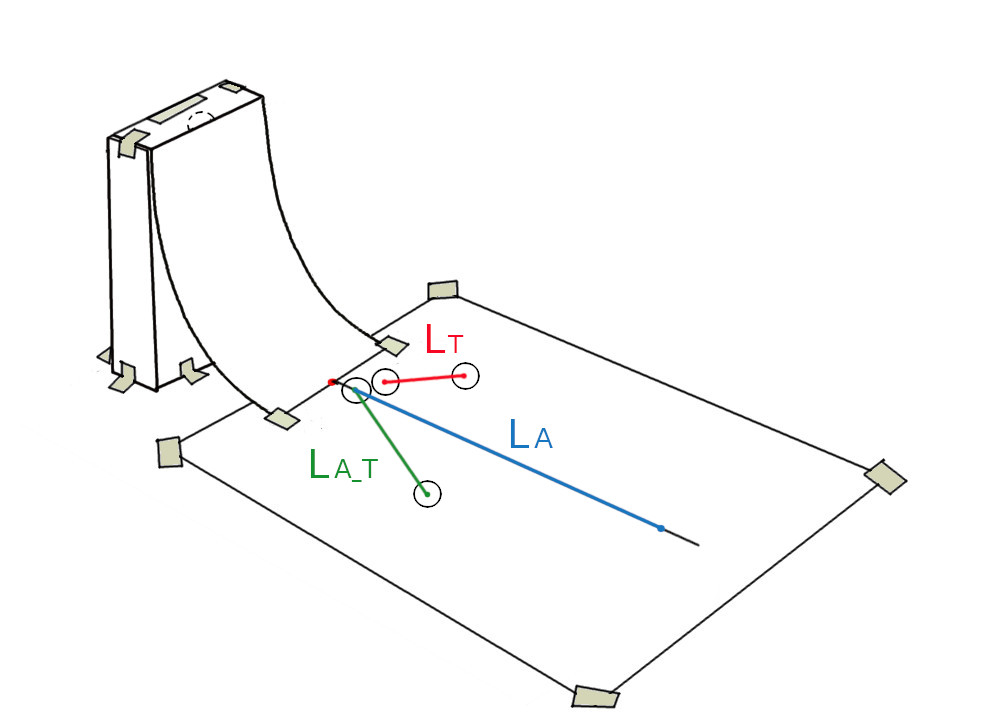
Fra poco vedremo come il principio possa essere esplorato quantitativamente con un dispositivo sperimantale interessante, sebbene composto solo da due fogli di carta A4, una scatoletta rigida (per esempio la scatola di un cellulare), alcune penne, una matita , del nastro adesivo di carta e due monete identiche da 1 centesimo.

L’idea dell’esperimento è accelerare una moneta (moneta Accelerata) con uno scivolo gravitazionale e poi farla collidere su un foglio orizzontale con una moneta bersagilo (moneta Target) inizialmente ferma. Alla base dell’esperimento sta un semplice concetto:
dai tragitti percorsi dalle monete su un foglio di carta orizzontale, possiamo ricavare molte informazioni sulla velocità che esse avevano nel punto iniziale del percorso stesso.
Le direzioni e i versi delle velocità sono date dalle direzioni e dai versi dei segmenti. I moduli delle velocità sono proporzionali alla radice quadrata delle lunghezze L dei segmenti. Ciò si spiega tenendo a mente che il lavoro fatto dalla forza di attrito lungo la traiettoria L della moneta è uguale, in modulo, all’energia cinetica persa dalla moneta lungo il tragitto:
\( F L = \frac{1}{2}\cdot mv^2 \)
da cui
\( v \propto \sqrt{L} \)
La costante di proporzionalità, tra v e la radice di L, è la stessa per entrambi i corpi in quanto le monete sono identiche. Quindi essa rappresenta solo un fattore di scala. Il suo valore non ci interessa, si semplifica nell’equazione di conservazione.
In sostanza, misurando le lunghezze di tre traiettorie e calcolando la radice quadrata di \(L_A\, , L_{AT}\, ,L_T \), ricaviamo tre vettori proporzionali a \(\vec{v}_{A}\, , \vec{v}_{AT}\, ,\vec{v}_T \), rispettivamente la velocità della moneta Accelerata prima dell’urto, quella della moneta Accelerata dopo l’urto con il Target, quella della moneta Target dopo l’urto.

Siamo pronti per verificare la legge di conservazione della qdm!
Basterà scrivere l’equazione di conservazione nel nostro caso particolare e poi analizzare se e quanto i nostri dati sperimentali aderiranno ad essa. Esprimiamo la legge matematicamente. Indichiamo la moneta che è scesa lungo lo scivolo con il simbolo A (Accelerata) e la moneta bersaglio con T (Target), le quantità valutate prima dell’urto sono contrassegnate dalla ‘i‘, quelle dopo dalla ‘f‘:
\( m\cdot \vec{v}_{Ai} \,+\,\vec{0}\,=\, m\cdot \vec{v}_{Af} \,+\, m\cdot \vec{v}_{Tf} \)
Essendo le monete identiche le masse m sono state indicate con lo stesso simbolo e si semplificano. Se nell’urto vi è stata conservazione della qdm deve essere
\( \vec{v}_{Ai}\,= \vec{v}_{Af}\,+\, \vec{v}_{Tf}\)
Con l’aiuto di due squadrette da disegno tecnico possiamo facilmente effettuare la somma vettoriale delle due velocità finali e vedere se il vettore risultante è parallelo e uguale in modulo alla velocità totale iniziale, cioè a \(\vec{v}_{1\,in}\). Questo video Tutorial vi guiderà passo passo nella conduzione dell’epserimento.
Alcuni risultati ottenuti con l’Acceleratore Gravitazionale
Qui trovate l’articolo apparso sull’American Journal of Physics 88, 279 (2020), in cui abbiamo presentato l’acceleratore gravitazionale e come usarlo per esplorare la legge di conservazione della qdm in due dimensioni: https://doi.org/10.1119/10.0000518. Purtroppo, è a pagamento.
Unisciti al Canale Telegram per essere sincronizzato con questo Blog: https://t.me/Two_Penny_Physics
Segui i video sul Canale YouTube: http://www.youtube.com/c/LorenzoGalante